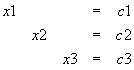Propiedades de las desigualdades.
1. Una desigualdad no cambia de sentido cuando se añade o se resta un mismo número a cada miembro
Efectivamente si en la desigualdad a > b se designa por "c" lo que falta a "b" para ser igual a "a", se tiene:
a = b + c
Añadiendo un mismo número, positivo o negativo a los miembros, se puede escribir:
a + m = b + c + m
Suprimiendo "c" en el segundo miembro, resulta evidentemente
a + m > b +m
Ejemplos:
9 > 5
9 + 2 > 5 + 2
11 > 7
-2 > -6
-2 -3 > -6 -3
-5 > -9
Consecuencia de esta propiedad: Puede suprimirse un término en un miembro de una desigualdad, teniendo cuidado de agregar en el otro miembro el término simétrico del suprimido; es decir, se puede pasar un término de un miembro a otro, cambiando su signo, porque esto equivale a sumar o restar una misma cantidad a los dos miembros.
Ejemplo:
6x -2 > 4x + 4
6x -4x > 4 + 2
2. Una desigualdad no cambia de sentido cuando se multiplican sus dos miembros por un mismo factor positivo, o se dividen entre un mismo divisor, también positivo.
Sea la desigualdad a > b, es decir, a = b + c
Multiplicando ambos miembros de la desigualdad por un número positivo "m", resulta:
am = bm + cm.
Suprimiendo el término positivo "cm", en el segundo miembro disminuye, y se tiene:
am > bm
Si "m" es recíproco de un número positivo, queda evidenciada la segunda parte de esta propiedad
Ejemplos:
12 > 7
12 * 3 > 7 * 3
36 > 21
15 > -25
15 ÷ 5 >(-25) ÷ 5
3 > -5
3. Una desigualdad cambia de sentido cuando se multiplican sus dos miembros por un mismo factor negativo, o se dividen entre un mismo divisor, también negativo.
Sea la desigualdad a > b, es decir, a = b + c
Multiplicando ambos miembros de la desigualdad por el factor negativo -n se obtiene:
-an = -bn -cn
Suprimiendo -cn, en el segundo miembro aumenta; por tanto,
-an < -bn
Si -n es recíproco de un número negativo, queda demostrada la segunda parte del enunciado.
Ejemplos:
3 > -15
3(-4) < (-15)(-4)
-12 < 60
64 < 80
64 ÷ (-4) >80 ÷ (-4)
-16 > -20
Consecuencia de la propiedad anterior pueden cambiarse todos los signos de una desigualdad, con tal que se cambie el sentido de la misma; porque esto equivale a multiplicar sus dos miembros por -1.
Ejemplo:
-7x + 130 < 9 -5x
7x - 130 > -9 + 5x
4. Si los dos miembros de una desigualdad son positivos y se elevan a la misma potencia, la desigualdad no cambia de sentido.
Sea la desigualdad a < b, en la que "a" y "b" son positivos. Multiplicando sus dos miembros por "b", resulta:
ab < b2
En el primer de esta desigualdad, sustituyendo "b" por "a", la desigualdad se refuerza; por tanto:
a2 < b2
Ejemplo:
7 < 10
73 < 103
343 < 1000
5. Si los dos miembros de una desigualdad son negativos y se elevan a una potencia de grado impar, no cambia el sentido de la desigualdad; pero hay cambio de sentido si el grado de la potencia es par.
Sea la desigualdad -a < -b
a) Multiplicando sus dos miembros por b2 se obtiene:
-ab2 < -b3
En el primer miembro, reemplazando b2 por a2, la desigualdad se refuerza; luego se puede escribir:
-a3 < -b3
b) Multiplicando los dos miembros de la primera desigualdad por -b y haciendo análogas transformaciones, la desigualdad cambia de sentido, porque sus términos cambian de signo, y se tiene:
a2 > b2
Ejemplos:
-3 > -6
(-3)3 > (-6)3
-27 > -216
-8 < -4
(-8)2 > (-4)2
64 > 16
6. Si se suman miembro a miembro varias desigualdades de mismo sentido, resulta una desigualdad de mismo sentido que aquéllas.
Sean las desigualdades a > b; a' > b'; a" > b"
Se puede escribir:
a = b + c
a' = b' + c'
a" = b" + c"
Sumando miembro a miembro y suprimiendo c + c' + c", se tiene, sucesivamente:
a + a' + a" = b + b' + b" + c + c' + c"
a + a' + a" > b + b' + b"
Ejemplo:
Dado: 2x > 10 y 7x > 26
se obtiene: 9x > 36
7. Si se restan miembro a miembro dos desigualdades de sentido contrario, resulta una desigualdad de igual sentido que el minuendo.
Sean las desigualdades a > b y c < d
Invirtiendo la segunda desigualdad y sumándola a la primera se tiene
a > b
d > c
---------------
a + d > b +c
Restando d + c de cada miembro, resulta:
a - c > b -d
Ejemplo:
Dado: 7x < 12 y 5x > 16,
se obtiene: 2x < -4