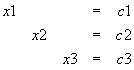Procedimiento:Primero se debe tener ya el sistema de ecuaciones que se quiere resolver y que puede ser de n numero de variables por ejemplo:
-3x+3y+2z=1
4x+y-z=1
x-2y+z=3
Y se acomodan los coeficientes y los resultados en una matriz:
El objetivo de este metodo es tratar de convertir la parte de la matriz donde estan los coeficientes de las variables en una matriz identidad que es una matriz con puros 0 y 1 pero los 1 estan en diagonal asi:
Esto se logra mediante simples operaciones de suma, resta y multiplicacion.Entoces, si se quiere convertir la primera matriz en la segunda, se puede observar que el -3 de la primera matriz se tiene que convertir en un 1, segun la matriz identidad, asi que hay que dividir entre -3, pero como una operacion se aplica a toda la fila, entonces toda la primera fila se tiene que dividir entre -3 y queda mas o menos asi:
Despues, como se ve en la matriz identidad, hay que hacer 0 toda la columna debajo del 1, y se hace multiplicando por algo la fila de arriba y sumandola a la fila de abajo, en este caso, si se multiplica por -4 la fila de arriba, la primera multiplicacion es -4x1, que sumado a la primera coordenada de la fila de abajo da el 0 que se desea, igualmente, la operacion se realiza con toda la fila por lo que a cada posicion de la fila de arriba se le multiplica por -4 y se suma con la correspondiente posicion de la fila de abajo. La siguiente multiplicacion seria -4x-1 y se sumaria con el 1 de abajo. La matriz va quedando de la siguiente manera:
En la imagen de al lado ya se termino de hacer 0 las posiciones que se requieren segun lo indica la matriz identidad.(Las R son por Row en ingles)
El siguiente paso para lograr una matriz identidad es obtener el siguiente 1, que en este caso iria en donde esta el 5 en la segunda fila. Como ya se trabajo con la primera columna ya no es necesario tomarla en cuenta puesto que se supone que ya esta bien.Para lograr un 1, hay que dividir toda la segunda fila (sin tomar en cuenta la primera columna) entre 5 y la matriz queda asi:
Despues se tienen que hacer 0 los que estan arriba y abajo del 1, que en este caso seria, para el que esta arriba 1xR2+R1 porque el R1 es un -1 y al sumarse con el 1 que da de la multiplicacion de 1xR2 da el 0 que se esta buscando.De igual manera para el que esta debajo es el mismo procedimiento porque en este ejemplo coincidio que los 2 fueran -1, pero hay que recordar siempre buscar el numero por el cual multiplicar para que a la hora de sumar de un 0.
Una vez que se obtuvieron los 0 solo falta obtener el ultimo 1 segun la matriz identidad. Esto se logra dividiendo entre 2 toda la tercera fila ignorando ya los que fueron hechos ceros.La matriz queda de la siguiente manera:
Por ultimo solo se hacen 0 los que estan encima del que acabamos de hacer 1, en este caso multiplicando por 1/3xR3 y sumandola a R1 para hacer el 0 que se necesita, y multiplicando -1/3xR3 y sumandolo a R2 para obtener el ultimo 0:
Como se podra notar, una matriz identidad siempre es cuadrada y al pasarla a nuestra matriz original sobro la columna donde iban los resultados de cada ecuacion, pues bien, esa ultima columna contiene los valores de las variables que se estan buscando y en orden, la de arriba es la primer variable, la de enmedio es la segunda y la ultima es la tercera.
. La matriz inversa de A es una matriz B de 
tal que:
para denotar la matriz inversa. Cuando la matriz inversa existe, es única, pro no siempre existe la matriz inversa.
existe si y solo si el determinante de A es distinto de cero.
del mismo orden que la matriz A; enseguida aplicamos el método de Gauss-Jordan para hacer los ceros y unos y obtener del lado izquierdo la matriz identidad 
. Del lado derecho lo que obtendremos será la matriz inversa de A. 
